Pour faire l'équation ƒ(x)Mr.Armand seules les symétries par l'axe (Ox) et (Oy) m'ont été utiles mais je mets quand même les autres pour le Fun !
La Symétrie par l'axe (Ox) ou (Oy) est toute simple :
Pour l'axe (Ox) il suffit de remplacer y = ƒ(x) par y = - ƒ(x) . Ainsi tout ce qui était sous l'axe (Ox) (lorsque y est négatif) passe au-dessus et inversement.
Pour L'axe (Oy) il suffit de remplacer y = ƒ(x) par y = ƒ(- x) . Ainsi tout ce qui était à gauche (donné par les valeurs négatives de x) passe à droite et inversement.
Sachant déjà comment déplacer la courbe horizontalement et verticalement on en déduit comment s'y prendre pour n'importe quels axes horizontales ou verticales.
Par exemple avec : y = x²,
pour sa symétrie par (Ox) on a : y = - x² ,
ensuite si l'on l'augmente de 2 on a : y = - x²+2 qui est symétrique à y = x² par l'axe y = 1 .
Pour avoir la symétrie par l'axe y = a on passe de y = ƒ(x) à y = - ƒ(x) +2a .
Attention, si l'on avait déplacé la courbe de 2a avant de faire sa symétrie par (Ox) on aurait eu :
y = ƒ(x) +2a (augmenter de 2a) puis y = - ( ƒ(x) +2a ) = - ƒ(x) -2a qui elle est symétrique par l'axe y = - a et pô par y = a !!!
Le même type de raisonnement amène à remplacer y = ƒ(x) par y = ƒ( -x -2b) pour avoir la symétrique par l'axe x = b .
La symétrie par le point conserve les distances et les directions ( l'image symétrique d'une droite lui est parallèle), mais inverse les sens !
Si l'on applique une symétrie horizontale et une verticale (quelques soit l'ordre dans lequel on procède) on a appliquer au final une symétrie par le point de rencontre des deux axes. Les axes y = a et x = b se rencontrent au point (b; a).
Du coup pour la symétrique de y = ƒ(x) par le point (b; a) c'est y = - ƒ( -x -2b) +2a .
Pour la symétrie par la diagonale y = x les valeurs de x et de y vont être inversés ! C'est à dire que la courbe symétrique à y = ƒ(x) va être l'ensemble de point (x; y) vérifiant x = ƒ(y) .
Par exemple la symétrique de y = x² est l'ensemble de point (x; y) tel que x = y² . Le problème est que l'on ne peut pô faire une fonction regroupant l'intégralité de ces points puisque pour chaque antécédent d'une fonction ne peut correspondre qu'une seule image au maximum (une ou aucune).
Cela se retrouve lorsque l'on cherche à ranger y seul de son côté :
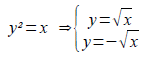
On est obligé de faire un choix ! Soit l'on prend la branche du haut soit celle du bas :
Pour l'autre diagonale y = - x tout sera inversé, pas seulement les x et les y mais carrément tous les sens.
Le plus simple est de faire d'abord une symétrie par le centre O (pour inverser les sens) suivis d'une par la diagonal y = x (pour inverser les valeurs x et y).
Ce qui donne : y = ƒ(x) → y = - ƒ( -x) → x = - ƒ( -y)
Exemple avec :
-Détails de calcul-
Pour la symétrie par le centre O (0;0), on passe à y = - ƒ( -x) :

Pour la symétrie par la diagonale y = x, la branche y = - x/2 donne x = - y/2 → y = -2x .
La branche y = - x²/2 donne :

Cette branche était défini pour x dans l'intervalle ] -∞ ; 0 [ . Après la symétrique elle l'est pour y → ] -∞ ; 0 [ et comme une racine carré sera toujours positive ou nul c'est l'équation y= - √(-2x) qui sera retenue.
Remarque : J'étais d'abord partie pour faire à ƒ une branche de type y = x + ( sin(xπ/2) )/2, je la trouvais très jolie (elle ressemble un peu à un escalier) ! Mais mes connaissances en trigo ne m'ont pô permis de résoudre : x = y + ( sin(yπ/2) )/2 , pourtant ça doit être possible !?
Du coup j'ai pris une ligne droite toute bête (y=-x/2). Si quelqu'un saurait comment résoudre ça, ça m'intéresse !
Histoire de finir, sachant comment déplacer les courbes on peut en déduire comment procéder pour n'importe quelle axe de symétrie parallèle à l'une des diagonales.
Prenons y = x+d (d étant un réel) qui est parallèle à y = x. On vois sur la figure que si l'on descend la courbe de d et qu'on l'avance de d sa symétrie par y = x sera celle que l'ont aurait eu par y = x+d. On a fait :
y = ƒ (x) → y = ƒ (x-d) – d → x = ƒ (y-d) – d
Ces symétries permettront de déduire quelques rotations. Mais pour des axes de symétrie avec des angles plus "exotiques" je ne sait pas encore. C'est aussi coton que trouvé comment faire des rotations "exotiques" (ce qui est normal puisque l'un permettrai de déduire l'autre et inversement !). Peut'être en passant par les coordonnées polaire ?! … Je ne sait pô encore …





Aucun commentaire:
Enregistrer un commentaire